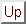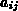 in der späteren Elimination der Matrixzeile
in der späteren Elimination der Matrixzeile 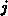 hängt vom Produkt
des Nebendiagonalelements
hängt vom Produkt
des Nebendiagonalelements 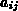 mit seinem symmetrischen Element
mit seinem symmetrischen Element
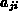 ab:
ab:

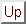


Die relative Skalierung der Matrixelemente hat großen Einfluß auf den Entscheidungsmechanismus, mit welchem der Präkonditionierer festlegt, welche Elemente der faktorisierten Matrix behalten und welche verworfen werden. Dieser Mechanismus heißt Dropping-Strategie.
Um das relative Gewicht von Matrixelementen zu ermitteln, ist die
Untersuchung eines elementaren Eliminationsvorgangs während der
Matrixfaktorisierung notwendig.
Das relative Gewicht eines Nebendiagonaleintrags 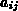 in der späteren Elimination der Matrixzeile
in der späteren Elimination der Matrixzeile 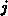 hängt vom Produkt
des Nebendiagonalelements
hängt vom Produkt
des Nebendiagonalelements 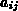 mit seinem symmetrischen Element
mit seinem symmetrischen Element
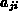 ab:
ab:
Wie man an der Matrixsubstruktur in Gleichung 8.4 erkennen
kann, hängt das relative Gewicht
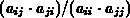 des hinzukommenden Matrixeintrags nicht von der Zeilen- oder
Spaltenskalierung ab.
Die Skalierung beeinflußt aber die Dropping-Strategie in der
Zeile
des hinzukommenden Matrixeintrags nicht von der Zeilen- oder
Spaltenskalierung ab.
Die Skalierung beeinflußt aber die Dropping-Strategie in der
Zeile 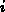 , die nur auf den Werten in dieser Zeile beruht.
Dem Verhältnis
, die nur auf den Werten in dieser Zeile beruht.
Dem Verhältnis 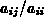 kann man jedoch durch Spaltenskalierung
jeden beliebigen Wert geben.
kann man jedoch durch Spaltenskalierung
jeden beliebigen Wert geben.
Es ist also eine Methode zu finden, wie man nur aufgrund der
relativen Größe der Matrixelemente in Zeile 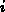 entscheiden kann,
welche Elemente bei der späteren Elimination den größeren Einfluß
haben.
entscheiden kann,
welche Elemente bei der späteren Elimination den größeren Einfluß
haben.
Um einen besseren Vergleich der Nebendiagonalelemente zu ermöglichen,
wird die Matrix zuerst durch Multiplikation mit Diagonalmatrizen von
links und von rechts so skaliert, daß die Elemente der Hauptdiagonale
alle 1 werden.
Der Effekt dieser ersten Skalierung ist, daß der neue Matrixbeitrag
nur von dem Produkt 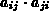 bestimmt wird.
bestimmt wird.
In der zweiten Phase wird versucht, die Nebendiagonalelemente der Matrix möglichst klein zu machen, wobei aber die Hauptdiagonalelemente auf 1 belassen werden sollen. Das geschieht, indem man je eine Zeile und die entsprechende Spalte gemeinsam so skaliert, daß sich die Hauptdiagonale nicht verändert, die Summe der Absolutwerte aller Nebendiagonalen aber so klein wie möglich wird. In einer Relaxation läuft man dabei mehrmals über alle Zeilen und Spalten der Matrix.
Nach etwa 4-6 Durchläufen sind die Nebendiagonalen gut äquilibriert, und die so gewonnene Skalierung unterstützt die Präkonditionierung deutlich, was sich in einem großen Zeitgewinn ausdrückt [P7].
Die Bilder 8.3 bis 8.5 geben den CPU-Zeit-Verbrauch
für ein typisches System mit 30207 Gleichungen auf einer
DEC ALPHA 7640 an. Kurvenparameter ist die erlaubte Anzahl von
Zusatzeinträgen pro Zeile in der faktorisierten Matrix (der
sogenannte fill-in), die Abszisse zeigt die Toleranzschwelle
für die Dropping-Strategie, die von 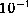 bis
bis 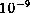 reicht. Das erste Bild gibt die Verhältnisse für ein unskaliertes
System an. Beim zweiten Bild wurden die Hauptdiagonaleinträge der
Matrix auf 1 skaliert; beim dritten wurden zusätzlich die
Nebendiagonalen unterdrückt.
reicht. Das erste Bild gibt die Verhältnisse für ein unskaliertes
System an. Beim zweiten Bild wurden die Hauptdiagonaleinträge der
Matrix auf 1 skaliert; beim dritten wurden zusätzlich die
Nebendiagonalen unterdrückt.