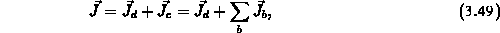



Von M. S. MOCK [53] stammt der Vorschlag, beim transienten Problem statt der Poisson-Gleichung eine Gesamtstromgleichung zu verwenden. Diese Gesamtstromgleichung berücksichtigt nämlich besser die Größe des Zeitschritts und die daraus resultierende Mischung der Ströme (des Verschiebungs- und des Leitungsstroms).
Die Gesamtstromdichte setzt sich aus dem Verschiebungsstrom (displacement current) und den Leitungsströmen (conduction currents) der einzelnen Trägertypen zusammen:
Die Gesamtstromgleichung
ergibt sich einfach aus der Überlagerung von Poisson- und
Kontinuitätsgleichungen , indem man die Poissongleichung nach der Zeit ableitet (die
Zeitableitung wird mit der Divergenzbildung vertauscht, was wegen der
Stetigkeit der Ableitungen zulässig ist):
, indem man die Poissongleichung nach der Zeit ableitet (die
Zeitableitung wird mit der Divergenzbildung vertauscht, was wegen der
Stetigkeit der Ableitungen zulässig ist):
Dazu wird der gesamte Leitungsstrom
addiert. Mit dem Zusammenhang zwischen Rekombination und Umladung der Störstellen,
ergibt die Summe der Divergenzen beider Ströme Null.
Im diskreten Fall kann der Gesamtstrom ganz analog aus der Zeitableitung der Poisson-Gleichung und dem Leitungsstrom zusammengesetzt werden. Im Sinn des Rückwärts-Euler-Schemas bildet man die Differenz von neuer Poisson-Gleichung (3.11) und ihrem alten Äquivalent, das so lautet:
Der Index ,, `` steht dabei wieder für die Werte der
entsprechenden Variablen zum vorigen Zeitpunkt, also am Beginn des
Zeitschritts.
`` steht dabei wieder für die Werte der
entsprechenden Variablen zum vorigen Zeitpunkt, also am Beginn des
Zeitschritts.
Die Differenz von (3.11) und (3.55) entspricht einer Gleichung für das Zeitintegral über den Verschiebungsstrom, also für die Ladungsveränderung. Der Differenzenquotient mit der Zeitschrittweite im Nenner beschreibt den diskreten Verschiebungsstrom:
Wenn man zu dieser Verschiebungsstromgleichung die Gesamtkontinuitätsgleichung für den Leitungsstrom addiert, die einfach aus einer Überlagerung aller Kontinuitätsgleichungen (3.35/3.36) entsteht,
fallen wieder die Quellterme weg, und übrig bleiben die Flußterme. Die so entstehende Gleichung ist die diskrete (auch zeitdiskrete) Gesamtstromgleichung:
Diese Gleichung kann jetzt im entkoppelten Schema statt der üblichen
Poisson-Gleichung verwendet werden. Das hat jedoch den Nachteil (siehe
O. HEINREICHSBERGER, [34]), daß in der
Poisson-Gleichung Ungenauigkeiten entstehen können, zum Beispiel
durch endliche Abbruchkriterien des Gleichungslösers. Da die
Poisson-Gleichung in dem Schema durch die Gesamtstromgleichung ersetzt
wurde, werden diese Ungenauigkeiten nicht durch ein Lösen der
Poisson-Gleichung behoben, sondern werden immer weiter mitgeschleppt,
weil in der Differenzen-Form in (3.56)
ein Fehler im alten Zeitschritt (in 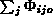 ) auch dem
neuen Zeitschritt aufgezwungen wird.
Die Lösung der Gesamtstromgleichung kann sich also, auch wenn man vom
Diskretisierungsfehler absieht, durch numerische
Rundungsfehler und besonders durch endliche Abbruchkriterien der
iterativen Lösungsprozesse für die einzelne Zeitschritte immer
weiter von der Lösung der Poisson-Gleichung entfernen.
) auch dem
neuen Zeitschritt aufgezwungen wird.
Die Lösung der Gesamtstromgleichung kann sich also, auch wenn man vom
Diskretisierungsfehler absieht, durch numerische
Rundungsfehler und besonders durch endliche Abbruchkriterien der
iterativen Lösungsprozesse für die einzelne Zeitschritte immer
weiter von der Lösung der Poisson-Gleichung entfernen.
Um einige wesentliche Vorteile dieser Gleichung im transienten Fall
doch übernehmen zu können, kann man mehrere Umwandlungen durchführen.
Statt der Gesamtstromgleichung läßt sich auch deren Zeitintegral,
das sich nur um den Faktor 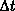 unterscheidet, als neue
Kontrollfunktion definieren:
unterscheidet, als neue
Kontrollfunktion definieren:
Die so entstandene Funktion besteht aus drei Teilen:
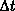 (der Zeitschrittweite) multiplizierten
Kontrollfunktionen der Kontinuitätsgleichungen.
(der Zeitschrittweite) multiplizierten
Kontrollfunktionen der Kontinuitätsgleichungen.
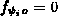 . Unter den weiteren Annahmen, daß im entkoppelten
Verfahren vor der Gesamtstromgleichung die Kontinuitätsgleichungen
gelöst wurden (und einander nicht oder nur schwach beeinflussen),
sind auch die
. Unter den weiteren Annahmen, daß im entkoppelten
Verfahren vor der Gesamtstromgleichung die Kontinuitätsgleichungen
gelöst wurden (und einander nicht oder nur schwach beeinflussen),
sind auch die 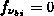 . Es bleibt nur der Wert der
Kontrollfunktion der aktuellen Poisson-Gleichung,
. Es bleibt nur der Wert der
Kontrollfunktion der aktuellen Poisson-Gleichung,
Der wesentliche Unterschied bei den Kontrollfunktionen der Gesamtstromgleichung und der Poisson-Gleichung besteht also weder im Funktionswert (der ist gleich), noch in der endgültigen Lösung für das Potential, die sie liefern, sondern einzig in der Ableitung nach den Variablen, insbesondere nach dem Potential:
Der Beitrag von 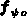 liefert selbstverständlich keine
Ableitungen nach dem aktuellen Potential.
liefert selbstverständlich keine
Ableitungen nach dem aktuellen Potential.
Man kann also statt der ursprünglichen Gesamtstromgleichung
die Mischvariante
mit dem neuen Poisson-Residuum 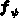 , aber den Ableitungen aus
der modifizierten Kontrollfunktion
, aber den Ableitungen aus
der modifizierten Kontrollfunktion 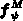 verwenden.
verwenden.
Im entkoppelten Verfahren mit Gesamtstromgleichung ist, wie bei der
GUMMEL-Variante der Poissongleichung, nach einer
Änderung des Potentials um 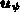 die Poissongleichung
(3.11) nicht erfüllt, weil die vorweggenommene
Änderung der Raumladung noch nicht eingetreten ist; wieder ist es dafür
notwendig, erst die Kontinuitätsgleichungen zu lösen.
die Poissongleichung
(3.11) nicht erfüllt, weil die vorweggenommene
Änderung der Raumladung noch nicht eingetreten ist; wieder ist es dafür
notwendig, erst die Kontinuitätsgleichungen zu lösen.
Dieser modifizierten Variante der Gesamtstromgleichung entspricht nun eine ähnliche physikalische Interpretation wie der GUMMEL-Variante der Poisson-Gleichung. In hochdotierten Gebieten, bzw. in Gebieten mit hoher Ladungsträgerkonzentration, wird eine Änderung der Potentialverhältnisse Einfluß auf den Strom haben, der von den Ladungsträgern transportiert wird:
Summation über alle Ladungsträger und die Definition einer
lokalen Leitfähigkeit 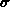 ergeben:
ergeben:
Wenn man die modifizierte Variante der Gesamtstromgleichung (3.63) nicht diskretisiert, sondern kontinuierlich berechnet, und (3.66) einsetzt, erhält man:
Diese Gleichung entspricht der Abschätzung, es würde sich durch das Zeitintegral über die Divergenz des zusätzlichen Leitungsstroms, der von dem Potentialinkrement hervorgerufen wird,
eine zusätzliche Raumladung 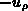 ergeben. Das ist genau die Aussage
der Kontinuitätsgleichungen. Man kann daher die Gesamtstromgleichung
(kontinuierlich (3.67) oder diskret (3.63))
interpretieren als eine Poisson-Gleichung, bei der die Änderung der
Raumladung durch das zusätzliche Potential mit Hilfe der
Kontinuitätsgleichungen abgeschätzt wurde. Gleichung 3.68
ist also gleichsam als Ableitungsvorschrift der Raumladung nach dem
Potential aufzufassen.
ergeben. Das ist genau die Aussage
der Kontinuitätsgleichungen. Man kann daher die Gesamtstromgleichung
(kontinuierlich (3.67) oder diskret (3.63))
interpretieren als eine Poisson-Gleichung, bei der die Änderung der
Raumladung durch das zusätzliche Potential mit Hilfe der
Kontinuitätsgleichungen abgeschätzt wurde. Gleichung 3.68
ist also gleichsam als Ableitungsvorschrift der Raumladung nach dem
Potential aufzufassen.
In Gebieten mit großer Ladungsträgerkonzentration wird laut
(3.67) der Potentialverlauf vollständig durch die
Leitfähigkeit bestimmt, in Gebieten ohne Ladungsträger und in
Isolatoren sowie in Verarmungsgebieten wird er durch die
Dielektrizität bestimmt. Der Übergang findet im Bereich
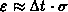 statt, ist also abhängig
von der Wahl des Zeitschritts.
statt, ist also abhängig
von der Wahl des Zeitschritts.
Bei extrem großen Zeitschritten, die über den längsten im Bauelement vorhandenen Zeitkonstanten liegen, oder bei stationären Problemen stellt die Gesamtstromgleichung verglichen mit der GUMMEL-Variante der Poisson-Gleichung die schlechtere Alternative dar, weil die Auswirkungen der Leitfähigkeit überschätzt werden. Bei sehr langen Zeitschritten findet ein eventueller Ausgleichsvorgang nämlich am Beginn des Zeitschritts einmal statt (hier kommt die Leitfähigkeit zum Tragen), und während des restlichen Zeitschritts ist der Ausgleich bereits vollendet.
Ein Beispiel, an dem das gut demonstriert werden kann, ist eine gesperrte Diode, an der die Sperrspannung geringfügig verändert wird (Bild 3.1). Der Leitfähigkeitsterm sagt für den ganzen Ohmschen Bereich (bis an den Rand der Raumladungszone) eine gleichmäßige Leitfähigkeit voraus, was zu dem gleichmäßigen Abbau eines (sehr geringen) Teils des Spannungshubes in diesem Bereich führt. Dagegen sagt die GUMMEL-Variante der Poisson-Gleichung eine Änderung der lokalen Ladungsträgerkonzentration mit dem lokalen Potential voraus. Dieses Verhalten führt dazu, daß an den Enden der Raumladungszone Potentialveränderungen und damit Ladungsträgerveränderungen auftreten, was mit der realen Verbreiterung oder Verschmälerung der Raumladungszone besser übereinstimmt.
Im allgemeinen ist es so, daß dauerhafte Veränderungen, die einmal aufgebaut werden und bestehen bleiben, besser durch die GUMMEL-Variante der Poissongleichung als durch die Gesamtstromgleichung beschrieben werden. Dazu zählen vor allem der Kanal im MOSFET sowie Raumladungszonen.
Es gibt also eine Grenze, über die nur schwer zahlenmäßige Feststellungen getroffen werden können, bei der der Zeitschritt so groß wird, daß man das Problem besser als stationär ansieht und die GUMMEL-Variante verwendet. Für die üblichen transienten Probleme wird die Gesamtstromgleichung aber bessere Dienste leisten. Bei der Festlegung eines Zeitschritts wird jedenfalls auch zu ermitteln sein, ob der Zeitschritt in der Größenordnung der größten Zeitkonstanten im Bauelement oder darunter liegt, oder ob er selbst die größten Zeitkonstanten noch übersteigt. Im letzteren Fall sollte die stationäre Variante gewählt werden. Die Sinnhaftigkeit eines solchen übergroßen Zeitschritts, sofern er nicht durch externe Einflüsse erzwungen wird, darf allerdings bezweifelt werden.
Für besonders kleine Zeitschritte degeneriert die Gesamtstromgleichung in der hier angegebenen Form zu einer reinen Poisson-Gleichung ohne spezielle Zusatzterme. Das ist gleichbedeutend mit einem Verschiebungsstrom, der durch einen Spannungssprung hervorgerufen wird, ohne daß im ersten Moment Ladungsverschiebungen auftreten.
Abschließend soll noch erwähnt werden, daß man gut daran tut, die
Leitfähigkeit 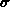 nicht aus den lokalen Parametern zu
ermitteln, sondern die Ableitungen der diskretisierten Ströme nach den
Gitterpunktspotentialen direkt zu bestimmen und zu verwenden, die man
ja ohnedies für das verkoppelte System braucht.
Damit wird nämlich statt der kontinuierlichen die diskrete
Kontinuitätsgleichung für die Änderung der Raumladung herangezogen,
und die Zusatzterme in der Gesamtstromgleichung sind konsistent mit
dem Rest des Gleichungssystems.
nicht aus den lokalen Parametern zu
ermitteln, sondern die Ableitungen der diskretisierten Ströme nach den
Gitterpunktspotentialen direkt zu bestimmen und zu verwenden, die man
ja ohnedies für das verkoppelte System braucht.
Damit wird nämlich statt der kontinuierlichen die diskrete
Kontinuitätsgleichung für die Änderung der Raumladung herangezogen,
und die Zusatzterme in der Gesamtstromgleichung sind konsistent mit
dem Rest des Gleichungssystems.