2.4.2 Die unstrukturierte Gitterinformation



Next: 3 Die Diskretisierung der
Up: 2.4 Das Gitter und
Previous: 2.4.1 Finite Boxen
Im Gegensatz zu reinen Finite-Differenzen-Diskretisierungen steht
bei Finiten Boxen in der vorliegenden Implementierung keine geordnete
Information über die Nachbarschaft des Punktes zur Verfügung. Es ist
also nicht möglich, falls beispielsweise ein Gitterpunkt mit einem
Nachbarn gegeben ist, auf einfache Art einen gegenüberliegenden
Nachbarn anzugeben, oder den nächsten im Uhrzeigersinn,
oder ähnliches.
Für die Diskretisierung der hier behandelten Gleichungen ist
allerdings eine solche Information nicht nötig. Man kommt dabei mit
einer unstrukturierten Nachbarschaftsinformation, das heißt, mit
einer einfachen Summation, die sich über alle Nachbarn erstreckt,
immer aus. Ein funktionaler Zusammenhang zwischen verschiedenen
Nachbarn, zum Beispiel solchen, die ihrerseits benachbart sind, ist
nicht vorhanden.
Probleme bereitet allerdings die Diskretisierung von Vektorgrößen.
Diese Diskretisierung spielt nur für abgeleitete Ausgabegrößen
und zur Bestimmung einzelner Hilfsgrößen (zum Beispiel der
Beweglichkeit in Abhängigkeit von der treibenden Kraft) eine Rolle,
findet also keinen Eingang in die Diskretisierung der eigentlichen
Differentialgleichungen.
Für die Diskretisierung von Vektorgrößen konnte eine
Formulierung gefunden werden, die ebenfalls nur unstrukturierte
Nachbarschaftslisten benötigt und für den Spezialfall von
Rechtecksgittern mit der bei diesen verwendeten Diskretisierung
übereinstimmt. Sie ist in Kapitel 5 angegeben.
Der Vorteil einer unstrukturierten Nachbarschaftsinformation liegt in
der Unabhängigkeit von der Struktur des Gitters. Es ist sehr leicht
möglich, neuartige Vergitterungsverfahren an den Simulator
anzubinden, weil vom Gitter keine spezielle Struktur verlangt wird.
In den Beispielen wurden die geometrischen Daten mit einem
Rechtecksgitter aufgelöst. Besonders beim HEMT entspricht ein
Rechtecksgitter am besten dem strukturellen Aufbau des Bauelements,
das aus sehr dünnen, parallelen Schichten besteht. Da die
MOS-Transistoren des Ringoszillator-Beispiels einen planaren Aufbau
besitzen, kommt man ebenfalls mit einem Rechtecksgitter aus.
Die strukturelle Information über das Gitter findet allerdings nur
Eingang in den Gittergenerator des Simulators. Das Ergebnis der
Vergitterung, das Rechengitter und die geometrische
Nachbarschaftsinformation, wird vom Rest des Programms ohne Kenntnis
der Gitterstruktur, nur auf der Grundlage der unstrukturierten
Nachbarschaftsinformation eines Finite-Boxen-Gitters, verwendet. Zur
Behandlung anderer Geometrien, die Dreiecksgitter erfordern, ist es
also nur erforderlich, die dem Gitter entsprechende
Nachbarschaftsinformation zu erzeugen.
Diese unstrukturierte Nachbarschaftsinformation besteht im
wesentlichen aus folgenden Daten, die in Listen zusammengefaßt sind:
- Für jeden Gitterpunkt:
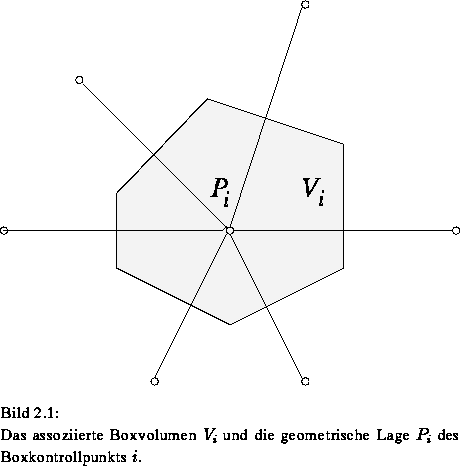
Die Gitterinformation enthält pro Gitterpunkt den Index 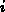 des Gitterpunkts/der Box, das zugeordnete Boxvolumen
des Gitterpunkts/der Box, das zugeordnete Boxvolumen 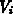 und den geometrischen Ort
und den geometrischen Ort 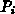 des Punktes
des Punktes 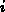 (Bild 2.1).
(Bild 2.1).
- Für jedes Paar benachbarter Boxen:
Für jedes Paar benachbarter Boxen werden die Indizes 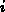 und
und
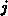 der beiden Gitterpunkte/der Boxen, die zugeordnete Distanz
der beiden Gitterpunkte/der Boxen, die zugeordnete Distanz
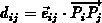 der Boxkontrollpunkte
der Boxkontrollpunkte 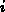 und
und 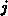 (diese Distanz allein
wird selten benötigt) und das Verhältnis der gemeinsamen
Boxgrenzfläche
(diese Distanz allein
wird selten benötigt) und das Verhältnis der gemeinsamen
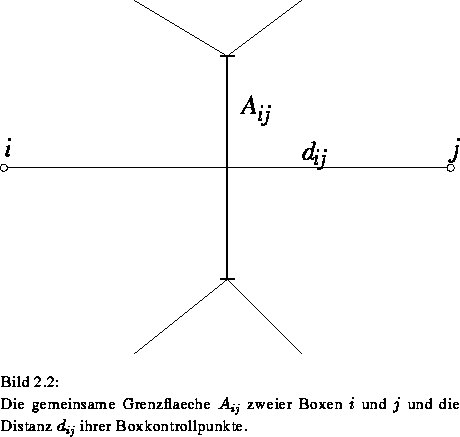
Boxgrenzfläche 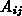 zu dieser Distanz:
zu dieser Distanz: 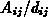 (Bild 2.2) zur Verfügung gestellt.
(Bild 2.2) zur Verfügung gestellt.
- Für Gitterpunkte auf Grenzschichten:
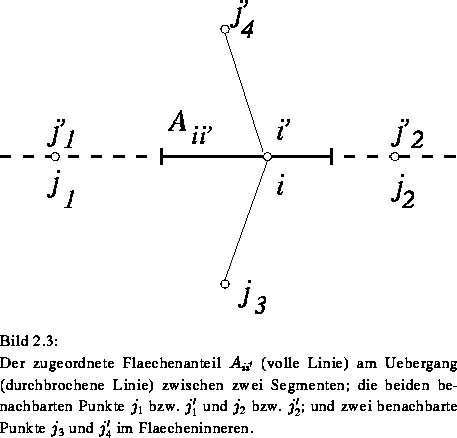
An Grenzschichten (Bild 2.3) gibt es jeweils Paare
benachbarter Boxen
mit den Kontrollpunkten 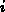 und
und 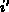 (diese Punkte haben
typischerweise den gleichen geometrischen Ort, sind aber
Kontrollpunkte verschiedener Boxen, die sich auf den beiden
Seiten der Grenzschicht erstrecken).
Für die beiden Kontrollpunkte gelten auch im allgemeinen
verschiedene Werte der Simulationsvariablen; jeder Wert ist als
einseitiger Grenzwert bei Annäherung an die Grenze von
der Seite seiner zugeordneten Box aus zu verstehen.
Die Simulationsvariablen werden auf der Grenzschicht im
allgemeinen durch Übergangsbedingungen verknüpft
(Kapitel 6).
(diese Punkte haben
typischerweise den gleichen geometrischen Ort, sind aber
Kontrollpunkte verschiedener Boxen, die sich auf den beiden
Seiten der Grenzschicht erstrecken).
Für die beiden Kontrollpunkte gelten auch im allgemeinen
verschiedene Werte der Simulationsvariablen; jeder Wert ist als
einseitiger Grenzwert bei Annäherung an die Grenze von
der Seite seiner zugeordneten Box aus zu verstehen.
Die Simulationsvariablen werden auf der Grenzschicht im
allgemeinen durch Übergangsbedingungen verknüpft
(Kapitel 6).
Für diese Übergangsbedingungen sind als Information die Indizes
der beiden Punkte 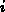 und
und 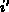 , der zugeordnete
Flächenanteil
, der zugeordnete
Flächenanteil 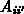 an der Grenzfläche, die Indizes
der beiden benachbarten Gitterpunkte an der Grenzschicht, und zwei
benachbarte Punkte im Flächeninneren vorhanden.
Die letztere Information ist aber nur bei besonders
komplizierten Übergangsbedingungen notwendig; für die im
Rahmen dieser Arbeit verwendeten vereinfachten
Übergangsmodelle wird sie nicht benötigt.
an der Grenzfläche, die Indizes
der beiden benachbarten Gitterpunkte an der Grenzschicht, und zwei
benachbarte Punkte im Flächeninneren vorhanden.
Die letztere Information ist aber nur bei besonders
komplizierten Übergangsbedingungen notwendig; für die im
Rahmen dieser Arbeit verwendeten vereinfachten
Übergangsmodelle wird sie nicht benötigt.
Diese Information, die praktisch keine Einschränkungen an den
Gittertyp stellt, reicht für die Diskretisierung der
Differentialgleichungen, die Formulierung der Randbedingungen und für
die Diskretisierung von Vektorgrößen aus.



Next: 3 Die Diskretisierung der
Up: 2.4 Das Gitter und
Previous: 2.4.1 Finite Boxen
Martin Stiftinger
Fri Oct 21 18:22:52 MET 1994
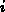 des Gitterpunkts/der Box, das zugeordnete Boxvolumen
des Gitterpunkts/der Box, das zugeordnete Boxvolumen 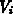 und den geometrischen Ort
und den geometrischen Ort 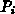 des Punktes
des Punktes 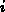 (Bild 2.1).
(Bild 2.1).
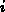 und
und
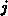 der beiden Gitterpunkte/der Boxen, die zugeordnete Distanz
der beiden Gitterpunkte/der Boxen, die zugeordnete Distanz
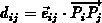 der Boxkontrollpunkte
der Boxkontrollpunkte 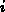 und
und 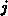 (diese Distanz allein
wird selten benötigt) und das Verhältnis der gemeinsamen
Boxgrenzfläche
(diese Distanz allein
wird selten benötigt) und das Verhältnis der gemeinsamen
Boxgrenzfläche 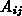 zu dieser Distanz:
zu dieser Distanz: 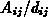 (Bild 2.2) zur Verfügung gestellt.
(Bild 2.2) zur Verfügung gestellt.
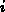 und
und 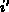 (diese Punkte haben
typischerweise den gleichen geometrischen Ort, sind aber
Kontrollpunkte verschiedener Boxen, die sich auf den beiden
Seiten der Grenzschicht erstrecken).
Für die beiden Kontrollpunkte gelten auch im allgemeinen
verschiedene Werte der Simulationsvariablen; jeder Wert ist als
einseitiger Grenzwert bei Annäherung an die Grenze von
der Seite seiner zugeordneten Box aus zu verstehen.
Die Simulationsvariablen werden auf der Grenzschicht im
allgemeinen durch Übergangsbedingungen verknüpft
(Kapitel 6).
(diese Punkte haben
typischerweise den gleichen geometrischen Ort, sind aber
Kontrollpunkte verschiedener Boxen, die sich auf den beiden
Seiten der Grenzschicht erstrecken).
Für die beiden Kontrollpunkte gelten auch im allgemeinen
verschiedene Werte der Simulationsvariablen; jeder Wert ist als
einseitiger Grenzwert bei Annäherung an die Grenze von
der Seite seiner zugeordneten Box aus zu verstehen.
Die Simulationsvariablen werden auf der Grenzschicht im
allgemeinen durch Übergangsbedingungen verknüpft
(Kapitel 6).
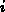 und
und 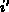 , der zugeordnete
Flächenanteil
, der zugeordnete
Flächenanteil 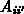 an der Grenzfläche, die Indizes
der beiden benachbarten Gitterpunkte an der Grenzschicht, und zwei
benachbarte Punkte im Flächeninneren vorhanden.
Die letztere Information ist aber nur bei besonders
komplizierten Übergangsbedingungen notwendig; für die im
Rahmen dieser Arbeit verwendeten vereinfachten
Übergangsmodelle wird sie nicht benötigt.
an der Grenzfläche, die Indizes
der beiden benachbarten Gitterpunkte an der Grenzschicht, und zwei
benachbarte Punkte im Flächeninneren vorhanden.
Die letztere Information ist aber nur bei besonders
komplizierten Übergangsbedingungen notwendig; für die im
Rahmen dieser Arbeit verwendeten vereinfachten
Übergangsmodelle wird sie nicht benötigt.