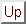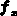Das Gleichungssystem, das man aus den diskretisierten Halbleitergleichungen erhält, ist hochgradig nichtlinear. Es muß mit Hilfe eines Iterationsverfahrens gelöst werden.
Zu diesem Zweck beginnt man mit einer geeigneten Anfangslösung, auf die später noch eingegangen wird. Für diese Anfangslösung werden die Werte der Kontrollfunktionen ausgerechnet; diese sind nicht Null, sondern geben das sogenannte Residuum der Gleichungen.
Indem man die Ableitungen der Kontrollfunktionen nach den
Variablen bestimmt, linearisiert man das System um den
momentanen Zustand, der noch inkonsistent ist.
Den Funktionsvektor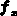 
der Kontrollfunktionen kann man durch
eine TAYLOR-Entwicklung um den momentanen Zustand
beschreiben:
Dabei bezeichnet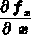 
die
Matrix, gebildet
aus den partiellen Ableitungen der Gesamtkontrollfunktionen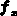
nach den Variablen , die sogenannte
JACOBI-Matrix. Der Vektor enthält die
Variablen im momentanen Zustand,
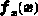sind die Gesamtkontrollfunktionen, die sich
nach dem Aufbau des Gleichungssystems in der rechten Seite befinden.
Für das NEWTON-Verfahren bricht man die Reihe nach der ersten Ableitung ab und setzt den Ausdruck gleich Null. Das ergibt die Gleichung
Man erhält in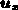 
eine Änderung des momentanen Zustands
, für welche die TAYLOR-Entwicklung das Residuum
Null ergibt.
Durch Addition dieses Inkrementsvektors ergibt sich ein neuer Zustand:
Im linearen Fall wäre das bereits die Lösung des Gleichungssystems.
Im nichtlinearen Fall ergibt sich allerdings durch die Terme höherer
Ordnung eine Verzerrung der Funktion.
Durch verschiedene Dämpfungsstrategien versucht man,
geeignet weit in Richtung des Vektors 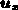fortzuschreiten,
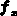sodaß die Norm des Vektors möglichst verkleinert wird.
Danach wiederholt man das Aufstellen des Gleichungssystems und den
Lösungsvorgang. Man bricht ab, wenn entweder die Norm des
Änderungsvektors 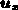oder die Norm des Funktionsvektors
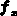oder beide genügend klein sind.
Damit man mit dieser Methode letztendlich bei der (oder bei einer) Lösung des Gleichungssystems anlangt, ist zweierlei erforderlich:
