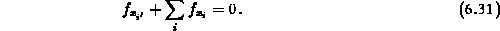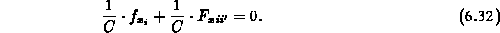6.5.5 Generalisierte Vorgangsweise



Next: 7 Verkoppelte Simulation
Up: 6.5 Allgemeine Randbedingungen
Previous: 6.5.4 Implizite Behandlung expliziter
Aus den letzten Überlegungen läßt sich eine allgemeingültige
Vorgangsweise gewinnen, die nicht nur für Heteroübergänge, sondern
auch für Ohmsche Kontakte geeignet ist.
An der impliziten Behandlung fällt auf, daß man zwei durchaus
verschiedenartige Gleichungen erhält, die man willkürlich den beiden
Boxen zuordnen kann. Es werden nicht beide Gleichungen gleich
diagonaldominant sein, und daher ist es meistens nicht günstig, die
Lösung beider Gleichungen einem iterativen Löser zu überlassen.
Eine der beiden Gleichungen wird also (wie beschrieben) aus dem
Gleichungssystem eliminiert, und mit ihr die dazugehörige Variable.
Die Vorgangsweise ist unsymmetrisch, da man willkürlich eine der
beiden Gleichungen wählen muß, wenn auch das Ergebnis
in der Kondition und der Struktur der Systemmatrix nur geringe (bei
der Poisson-Gleichung beispielsweise gar keine) Unterschiede zeigt.
Die zur Elimination gewählte Variable verschwindet dann aus dem
Gleichungssystem.
Das folgende allgemeine Schema kann man auch bei Ohmschen Kontakten,
also bei DIRICHLET-Randbedingungen mit
Kontaktstromintegration, einhalten:
- Wahl der Variablen, die eliminiert werden soll.
Im weiteren wird sie als
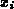 bezeichnet.
In einigen Fällen von Randbedingungen wird es notwendig sein,
eine der beiden Variablen zu bevorzugen; bei den hier
besprochenen Formeln für Materialübergänge kann die
Wahl nach zufälligen Kriterien erfolgen.
bezeichnet.
In einigen Fällen von Randbedingungen wird es notwendig sein,
eine der beiden Variablen zu bevorzugen; bei den hier
besprochenen Formeln für Materialübergänge kann die
Wahl nach zufälligen Kriterien erfolgen.
- Weiterleiten der Kontrollfunktion dieser Variablen
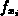 zur Box einer gegenüberliegenden Variablen
zur Box einer gegenüberliegenden Variablen 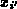 . Dadurch
entsteht eine Gleichung für die Gesamtkontrollfunktion der
Variablen
. Dadurch
entsteht eine Gleichung für die Gesamtkontrollfunktion der
Variablen 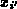 , also für die Gesamtbox:
, also für die Gesamtbox:
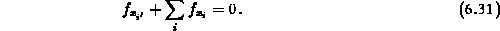
- In der Box
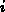 (der eigenen Box):
(der eigenen Box):
Abschwächen der Kontrollfunktion der eigenen (der zu
eliminierenden) Variablen. Für den Fall, daß kein expliziter
Fluß gegeben ist, wird mit dem Faktor 0 multipliziert (das
heißt, die eigene Kontrollfunktion verschwindet gänzlich aus
der eigenen Gleichung). Für den Fall eines explizit gegebenen
Flusses der Form ähnlich (6.29) kann man mit 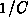 abschwächen, um die Gleichungskoeffizienten der resultierenden
Gleichung in die Größenordnung 1 zu bringen, oder man kann mit
dem Faktor 1, also gar nicht, abschwächen, und das Problem dem
Gleichungsskalierer überlassen.
abschwächen, um die Gleichungskoeffizienten der resultierenden
Gleichung in die Größenordnung 1 zu bringen, oder man kann mit
dem Faktor 1, also gar nicht, abschwächen, und das Problem dem
Gleichungsskalierer überlassen.
- In der Box
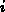 (der eigenen Box):
(der eigenen Box):
Addieren der Ersatzgleichung (wenn kein expliziter Fluß gegeben
ist) oder Addieren des ebenfalls abgeschwächten Flusses zur
abgeschwächten Kontrollfunktion. Das Ergebnis ist die
Boxgleichung, mit der die eigene Variable aus dem System eliminiert
wird.
Diese lautet bei explizit gegebenem Fluß 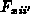 ,
wenn zum Beispiel mit dem Faktor
,
wenn zum Beispiel mit dem Faktor 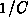 abgeschwächt wurde,
abgeschwächt wurde,
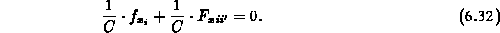
Wenn dagegen der Fluß nicht explizit gegeben ist, ist die
Boxgleichung einfach die reine Ersatzgleichung, da die eigene
Kontrollfunktion mit dem Faktor 0 ausgelöscht wurde. Im Fall
der Poisson-Gleichung lautet die Boxgleichung also einfach

Allgemein läßt sich dieser Punkt als das Addieren von
Zusatztermen zur eigenen Gleichung interpretieren.
- Elimination der eigenen Variablen mit der Boxgleichung aus
dem Gesamtsystem.
In diesem Schema wird durch die Summation in Gleichung 6.31
die Tatsache berücksichtigt, daß mehrere Randboxen die eigene
Kontrollfunktion zu derselben gegenüberliegenden Box weiterleiten
können. Ein Beispiel dafür ist der Ohmsche Kontakt, an dem der Strom
durch genau diese Weiterleitung der Kontrollfunktionen der
angrenzenden Boxen in einer ,,Kontaktbox`` gesammelt wird.
In diesem Zusammenhang soll noch darauf hingewiesen werden, daß die
Box, zu der weitergeleitet wird, durchaus nicht eine gleichartige
Größe als Boxvariable besitzen muß; so wird am Kontakt der
dielektrische Fluß, der in den Kontrollfunktionen der angrenzenden
Boxen berechnet wird, nicht zum Kontaktpotential der Kontaktbox
weitergeleitet, sondern zu deren Oberflächenladung.
Eine detaillierte Erörterung der Kontaktgrößen
ist allerdings hier fehl am Platz, sie werden in Kapitel 7
besprochen.
Diesem allgemeinen Schema entsprechen die folgenden Methoden bei der
Assemblierung des Gleichungssystems (siehe Kapitel 8, in dem
die Zeilentransformation vorgestellt wird):
- Setzen eines Flags für die zu eliminierende Variable.
- Definition einer entsprechenden Zeilentransformation zum
Weiterleiten der Kontrollfunktion.
- Das Abschwächen ist ebenfalls durch die Zeilentransformation
beschrieben.
- Addition von Gleichungsbeiträgen, die die Zeilentransformation
nicht durchlaufen.
- Die Elimination wird vom Gleichungsassembler automatisch
durchgeführt, da die entsprechende Gleichung zur Elimination
markiert wurde.



Next: 7 Verkoppelte Simulation
Up: 6.5 Allgemeine Randbedingungen
Previous: 6.5.4 Implizite Behandlung expliziter
Martin Stiftinger
Fri Oct 21 18:22:52 MET 1994
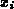 bezeichnet.
In einigen Fällen von Randbedingungen wird es notwendig sein,
eine der beiden Variablen zu bevorzugen; bei den hier
besprochenen Formeln für Materialübergänge kann die
Wahl nach zufälligen Kriterien erfolgen.
bezeichnet.
In einigen Fällen von Randbedingungen wird es notwendig sein,
eine der beiden Variablen zu bevorzugen; bei den hier
besprochenen Formeln für Materialübergänge kann die
Wahl nach zufälligen Kriterien erfolgen.
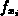 zur Box einer gegenüberliegenden Variablen
zur Box einer gegenüberliegenden Variablen 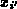 . Dadurch
entsteht eine Gleichung für die Gesamtkontrollfunktion der
Variablen
. Dadurch
entsteht eine Gleichung für die Gesamtkontrollfunktion der
Variablen 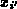 , also für die Gesamtbox:
, also für die Gesamtbox:
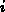 (der eigenen Box):
(der eigenen Box): 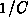 abschwächen, um die Gleichungskoeffizienten der resultierenden
Gleichung in die Größenordnung 1 zu bringen, oder man kann mit
dem Faktor 1, also gar nicht, abschwächen, und das Problem dem
Gleichungsskalierer überlassen.
abschwächen, um die Gleichungskoeffizienten der resultierenden
Gleichung in die Größenordnung 1 zu bringen, oder man kann mit
dem Faktor 1, also gar nicht, abschwächen, und das Problem dem
Gleichungsskalierer überlassen.
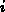 (der eigenen Box):
(der eigenen Box): 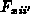 ,
wenn zum Beispiel mit dem Faktor
,
wenn zum Beispiel mit dem Faktor 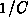 abgeschwächt wurde,
abgeschwächt wurde,